Digital week 4 (25/08/2015)

1.) สิ่งที่ได้จากการเรียนรู้

-Karnaugh Maps
     คือการลดรูปวงจร Logic Gate ที่ง่ายและรวดเร็วกว่ารูปแบบของ Boolean ซึ่งมีกฏ 3 ข้อในการทำดังนี้

1. การวงเลข ที่ได้ในตาราง Output นั้นต้องวงกลมในแนวตั้งหรือแนวนอนเท่านั้น
2. เลขที่อยู่ในวงนั้น จะต้องมีจำนวนของตัวเลข = 2ยกกำลัง(n)
3. ในการวงเลขนั้นจะต้องไม่มีตัวเลขที่ต่างกันเลยในวงกลม (เลือกทำแบบ SOP วง1ต้องไม่มี0 , เลือกทำแบบ POS วง0ต้องไม่มี1)

ตัวอย่างกรณี K-map 2 input

ตัวอย่างกรณี K-map 3 input

ตัวอย่างกรณี K-map 4 input

ตัวอย่างกรณี K-map 5-6 input เราจะมองเห็น K-map เป็นภาพ 3 มิติ

จากตัวอย่าง!!! มีข้อสังเกตได้ว่า....

• ตาราง 2-4 input จะเป็นตาราง K-map แบบ 2 มิติ
• จำนวนช่องตารางในการสร้าง K-map จะเท่ากับจำนวน input ยกกำลัง 2
• การสร้างตาราง K-map นั้น เราจะเลือกใส่ input ใดมาก่อนหรือหลังก็ได้ เพียงแต่ต้องครบตามตาราง Truth Table ที่เราได้กำหนดไว้ในตอนแรก เช่น มี input = A,B,C จะเลือก AB,C หรือ A,BC หรือ AC,ฺB ก็ได้
• จำนวน input ตั้งแต่ 5 input ขึ้นไป ตาราง K-map จะเป็นแบบ 3 มิติ ในกรณีนี้หากทำการคำนวณจริงๆจะเห็นว่า จะมีความยุ่งยากในการสร้างตาราง K-map มากขึ้น ดังนั้น หากมี input มากกว่า 5-6 input ขึ้นไป แนะนำว่าควรใช้โปรแกรมในการคำนวณจะทำให้มีความผิดพลาดน้อยและรวดเร็วกว่ามาก

คุณสมบัติเพิ่มเติมของ K-map ที่ต้องทราบ!

--------------------------------------------------------------------------------------------------------------------------

--------------------------------------------------------------------------------------------------------------------------

1. ตาราง K-map จากภาพตัวอย่างนั้น สามารถที่จะม้วนหรือจับมุมทั้ง 4 ด้านให้มาชนกันได้ นั้นหมายความว่า เราสามารถที่จะวงกลมตัวเลขที่เราม้วนแล้วมันมาติดกันได้ด้วย
2. หากเป็นตาราง 5 input ขึ้นไป จะเป็นตารางแบบ 3 มิติ ซึ่งเราก็สามารถที่จะวงกลมตัวเลขที่เหมือนกัน ในตำแหน่งที่ตรงกัน ในแต่ละตารางได้อีกด้วย แต่อย่าลืม!!! ตัวเลขที่จะวงกลมนั้น ต้องมีจำนวนตัวเลขในวงกลม เท่ากับ 2ยกกำลัง(n)
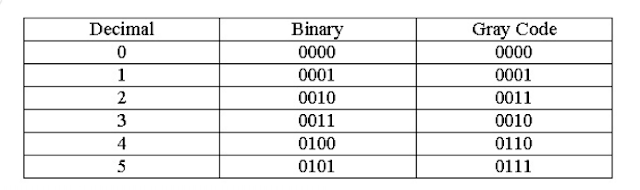
3. ตัวเลข (00,01,11,10) ที่อยู่ข้างตารางนั้น เป็นตัวเลขแบบ GrayCode ไม่ใช่ BinaryCode

-เกร็ดความรู้เพิ่มเติม

    GrayCode คือรหัสที่แต่ละค่าที่เปลี่ยนจะเปลี่ยนไปเพียง1บิตเสมอ เพื่อลดErrorในการส่งข้อมูล แต่ไม่เหมาะในการคำนวณ นิยมใช้กันมากในการนำมาประยุกต์ใช้กับการสร้างLogicต่างๆที่เกี่ยวข้องกับดิจิตอล

2.) ปัญหาที่พบ

- ยังไม่คล่องในการเขียน output ที่ดูจากการวง

-       - ยิ่ง input มีเยอะ ยิ่งต้องดูให้รอบคอบ อาจเกิดการผิดพลาดได้ง่าย

Digital week 3 (17/08/2015)

1.) สิ่งที่ได้จากการเรียนรู้

-การออกแบบวงจรจากโจทย์เพื่อให้ได้ Logic gate ตรงตามที่โจทย์กำหนด

  Ex.

-จะออกแบบวงจร Logic Gate นี้ได้อย่างไร?

• ทำ Truth table เพื่อคำนวณหา Output ที่เราต้องการ จากการใช้ Sensor จำนวณ 3 ตัว ซึ่งในกรณีนี้ หาก sensor 2 ใน 3 ตัว detect เจอเปลวไฟวงจรก็จะยังทำงานอยู่ และแสดงผลว่า sensor ทั้ง 3 ตัวยังใช้งานอยู่หรือไม่ โดยการแสดงผลจากหลอดไฟที่ต่อตรงเข้ากับ sensorแต่ละตัว
• เมื่อได้ Truth table เรียบร้อยแล้ว เราจะนำผลที่ได้จาก output มาเป็นสมการโดยการทำ "Boolean expression" , และลดรูปของสมการโดยเทคนิคของ "Boolean Algebra"  และเมื่อได้สมการที่ทำการลดรูปเรียบร้อยแล้ว จึงนำมาปรับรูปแบบ เป็น Logic Gate

***Let's Time to PLAY! (จากตัวอย่าง)

     เมื่อได้ Truth table แล้ว เราก็ นำผล Output เข้าสู่ "Boolean expression" ซึ่ง "Boolean expression" คือ การบวกกันของผลบวก เช่น AB +AC  แตกต่างกับ Truth table คือ จะแสดงเป็นสมการ ผลคูณ ผลบวก ต่างๆ และสามาถนำไปทำ Logic Gates ได้ นอกจากนี้วงจรที่ดูซับซ้อนมากๆ เรายังสามารถลดรูปของมันได้ โดยใช้เทคนิคของ Boolean Algebra 
     output1 จะใช้เทคนิค Sun of Product (SOP) และ output2 จะใช้ เทคนิค Product of Sum (POS) การทำเทคนิคทั้ง 2 มีวิธีดังนี้

-Sum of Product (SOP)

   โดยขั้นตอนการทำนั้น Sum of Product จะสนใจที่ Output เป็น 1 และเขียนเป็นสมการที่ คูณ กันก่อนแล้วจึงนำไป บวก กับ ค่าของ Input หากเป็นค่า 0 จะใส่เครื่องหมาย - ไว้ข้างบน input นั้น เมื่อได้สมการในค่า output ทั้งหมดแล้ว ให้นำแต่ละสมการที่ได้มา บวก กันในที่นี้ เราจะได้สมการคือ 

และนำไปทำเป็น Logic gate ได้ ดังนี้

จะสังเกตได้ว่า หากทำตาม Logic Gate ในรูป จะต้องใช้ OR Gate , AND Gate , NOR Gate หลายตัว และเราสามารถลดรูปวงจรนี้ได้อีก โดยมีวิธีการคือ ใช้ เทคนิค "Boolean Algebra" ดังนี้

        -เอกลักษณ์ของ Boolean (การบวก-การคูณ)

        -สมบัติของ Boolean

      -การลดรูปโดยใช้กฎของ Boolean

     จะได้ ขั้นตอนการลดรูปสมการ ดังนี้

     จากนั้น นำไปปรับเป็น Logic Gate ได้คือ 

     เราจะเห็นได้ว่า จากสมการที่ยาวๆ พอใช้เทคนิคของทั้ง "Boolean expression"  และ "Boolean Algebra" แล้ว จากLogic Gate ที่ต้องใช้ gate หลายๆตัวมาต่อกันก็จะลดลงอย่างมาก ทว่า Output ที่ได้ก็ยังคงเหมือนเดิม

-Product of Sum (POS)

     ต่างจากหารทำ Sum of Product (SOP) ตรงที่ Product of Sum (POS) จะสนใจ Output ที่มีค่าเป็น 0 และค่า Input หาก Input เป็น 1 ก็จะใส่ - ข้างบน  Input นั้น จากนั้นนำมา บวก กันก่อนแล้วจึง คูณ กัน ดังเช่นตัวอย่าง

-เพิ่มเติมม

ทำไมการคูณ ถึง แทนด้วย AND Gate , การบวก ถึง แทนด้วย OR Gate

Exclusive-OR คือ Gate ที่ หาก Input เหมือนกันจะได้ Output  = 0 หาก input ต่างกัน จะได้ Output = 1

2.) ปัญหาที่พบ

-ลดรูปสมการโดยใช้ Boolean ยังไม่ค่อยคล่องต้องหมั่นฝึกทำเยอะๆ

-ไม่ค่อยคล่องในการ ทำ Truth table เพื่อพิสูจน์ว่าสมการที่ได้ผ่านการลดรูปแล้ว Output จะตรงกับของเดิมหรือไม่

Digital week 2 (13/08/2015)

1.) สิ่งที่ได้จากการเรียนรู้

-การแปลงเลขฐานสิบเป็นเลขฐานสอง โดยวิธีการหารสั้น หรือหากแปลงเลขฐานอะไรแล้ว หากกระทำกลับแล้วจะได้ค่าของเลขฐานเช่นเดิม ซึ่งมันออกจะยากนิดหน่อยสำหรับ การดูว่า เลขฐาน10 นี่หากแปลงเป็นเลขฐาน2 แล้วจะมีค่าเท่าใด เนื่องจากในชีวิตประจำวัน เราใช้เลขฐาน10เป็นหลักในการกระทำสิ่งต่างๆ

-การบวกเลขฐาน2 (อันนี้ค่อยข้างเข้าใจได้ง่ายครับ)

-การทำ 2’s compliment (จำเป็นต้องทำในเลขที่เป็นค่าติดลบ) 
โดยเริ่มแรกจะทำการเปลี่ยนแปลงเลข 0 เป็นเลข 1 และแปลงเลข 1 เป็นเลข 0 หลังจากนั้นจะบวกด้วย  1 จะทำให้ได้ค่าลบในเลขฐานสองออกมา เพื่อนำไปใช้ในการบวกลบเลขฐานสองต่อไป ซึ่งหากเราทำงานร่วมกับเพื่อนร่วมงานคนอื่นๆ หากเป็นการบวกลบ ค่าแบบ 2’s compliment นั้น จำเป็นอย่างมากที่เราต้องแจ้งให้เพื่อนร่วมงานทราบว่า เรากำลังคำนวณค่าแบบ 2’s compliment

-Overflow
คือ การที่ค่าผลลัพธ์ของการบวกลบ มีค่าเกินกว่า Data range ที่จำนวนบิตของตัวแปรจะแสดงค่าได้ (หาก overflow หรือไม่ จำได้จาก จำนวนค่า Max , Min ของแต่ละบิต ว่ามีค่าสูงสุดต่ำสุดเท่าใด)

หรืออีกวิธีคือ (รูปภาพข่างล้าง)

***ให้ระวังด้วยเมื่อทำ 2’s compliment ประมาณว่า จะ Over Flow ถ้า CarryIn & CarryOut มีค่าต่างกันที่ MSB 

-เมื่อแปลงเป็น Logic Gate ก็จะได้ดังนี้ 

2.) ปัญหาที่พบ
 -มีอาการหลุด นั่งเหม่อ ขณะเรียนเรื่อง วงจร half adder และ full adder ทำให้ไม่ค่อยเข้าใจในเรื่องนี้ อยากให้ อาจารย์ช่วยอธิบายเพิ่มเติม ว่า หาก เราเลือกทำแต่วงจรที่เป็น Full Adder จะมีข้อดีข้อเสียต่างจาก Half Adder อย่างไร หรือ ข้อดีข้อเสียของทั้ง2วงจรนี้ ต่างกันอย่างไรครับ